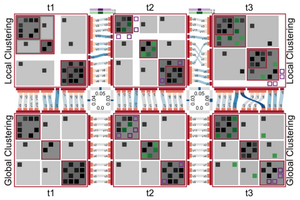
Type of Publication: Article in Journal

Visualizing Dynamic Hierarchies in Graph Sequences

Author(s):

Vehlow, Corinna; Beck, Fabian; Weiskopf, Daniel

Title of Journal:

IEEE Transactions on Visualization and Computer Graphics

Volume (Publication Date):

22 (2016)

Number of Issue:

10

pages:

2343-2357

Digital Object Identifier (DOI):

doi:10.1109/TVCG.2015.2507595

Fulltext:

Visualizing Dynamic Hierarchies in Graph Sequences (10.49 MB)

Citation:

Download BibTeX

Abstract

Graphs are used to model relations between objects, where these objects can be grouped hierarchically based on their connectivity. In many applications, the relations change over time and so does the hierarchical group structure. We developed a visualization technique that supports the analysis of the topology and the hierarchical group structure of a dynamic graph and the tracking of changes over time. Each graph of a sequence is visualized by an adjacency matrix, where the hierarchical group structure is encoded within the matrix using indentation and nested contours, complemented by icicle plots attached to the matrices. The density within and between subgroups of the hierarchy is represented within the matrices using a gray scale. To visualize changes, transitions and dissimilarities between the hierarchically structured graphs are shown using a flow metaphor and color coding. The design of our visualization technique allows us to show more than one hierarchical group structure of the same graph by stacking the sequences, where hierarchy comparison is supported not only within but also between sequences. To improve the readability, we minimize the number of crossing curves within and between sequences based on a sorting algorithm that sweeps through the sequences of hierarchies.